FUNCIÓN DE UNA VARIABLE REAL : DEFINICIÓN, DOMINIO Y RANGO DE UNA FUNCION CUADRÁTICA

Sean a, b y c números reales con a ≠ 0, la función f de R en R cuya regla de correspondencia es f (x) = ax² + bx + c , recibe el nombre de función cuadrática.
Su gráfica corresponde geométricamente a una parábola cóncava hacia arriba o hacia abajo.

FORMA CANÓNICA Y FACTORIZADA

FORMA CANÓNICA

Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:

$f(x) = a (x - h)^2 + k \,$

Siendo a el coeficiente principal y el par ordenado (h;k) las coordenadas del vértice de la parábola. Para llegar a esta expresión se parte de la forma polinómica y se completan cuadrados.

FORMA FACTORIZADA

Toda función cuadrática se puede factorizar en función de sus raíces. Dada:

$f(x) = ax^2 + bx + c \,$

se puede factorizar como:

$f(x) = a(x - x_1)(x - x_2) \,$

siendo a el coeficiente principal de la función, por ello se extrae siempre como factor común, de no escribirse, el coeficiente de x² sería siempre 1. x₁ y x₂representan las raíces de f(x). En el caso de que el Discriminante Δ sea igual a 0 entonces x₁ = x₂ por lo que podríamos escribir:

$f(x) = a(x - x_1)^2 \,$

En este caso a x₁ se la denomina raíz doble, ya que su orden de multiplicidad es 2.

DOMINIO Y RANGO

Como con cualquier función, el dominio de función cuadrática f(x) es el conjunto de los valores de x para los cuales la función esta definida, y el rango es el conjunto de todos los valores de salida (valores de f).

Las funciones cuadráticas generalmente tienen la recta real de enteros como su dominio: cualquier x es una entrada legítima. El rango esta restringido a esos puntos mayores que o iguales a la coordenada en y del vértice (o menores que o iguales a, dependiendo si la parábola abre hacia arriba o hacia abajo).

EJEMPLO

Determinar Dominio y Rango de f(x) = x2 - 2x – 3
Tabulamos valores de los pares ordenados x,y para representarlos en el plano cartesiano:

Ahora ubicamos cada pareja en el plano y unimos los puntos para obtener la gráfica de nuestra función.

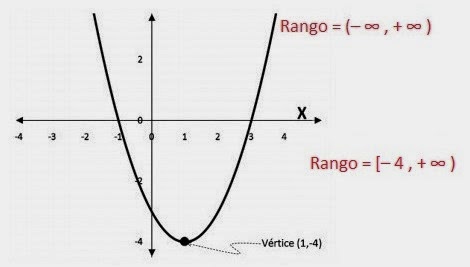Figura 1
Obtenido(http://matematicasdelbachillerato.blogspot.com/p/funciones-dominio-rango-y-graficas.html)

Como podemos ver, la gráfica es una parábola. Este tipo de función se conoce como cuadrática y representa a los polinomios de grado 2.

Dominio de la función
Como es una función polinómica de segundo grado el dominio será todo el conjunto de los números reales (siempre tomará valores tanto negativos como positivos en el eje x).

Dom f(x) = R

RANGO DE UNA FUNCIÓN

Note cómo la gráfica empieza a tomar valores en el eje y sólo a partir de un punto determinado. ¨Por lo tanto, en este caso, el rango ya no serán todos los reales.

Para hallar el Rango, debemos determinar a partir de qué punto la función empieza a tomar valores en el eje y.Esto ocurre en el vértice de la función.

El vértice de una función cuadrática se define como (-b /2a, f(-b, 2a)) reemplazando valores tenemos que -b /2a = (-(-2) / 2(1)) = 1. Este es el valor de x en el vértice.

Ahora reemplazamos este valor de x en la función original para conocer el valor de y en el vértice:
f(1) = 12 - 2(1) – 3 = 1- 2 - 3 = - 4

Por lo tanto, el vértice está en el punto (1, - 4).

El eje “Y” empieza a tomar valores (de abajo hacia arriba) a partir de -4.

Rango = [– 4 , + ∞ )

* El paréntesis cerrado [ o ] significa que el valor está incluido en el intervalo.
* El paréntesis abierto ( o ]) significa que el valor no está incluido en el intervalo.